Pattern forming mechanism in 'traveling wave' patterned mice

Stripes moving across the face of a single mouse in traveling waves.

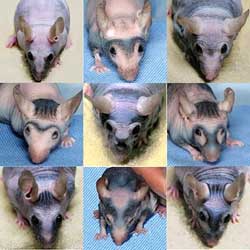
The research described in the PNAS article began when Kondo, whose research focuses on identifying the bases of biological pattern formation, was told about a mutant strain of mouse with an unusual striped phenotype. The mutation, a splicing defect in the Foxn1 (Whn or nude) gene, results causes hair follicle development to terminate just after skin pigments begin to accumulate. The immature follicles die off and are quickly replaced by a new hair cycle. The cyclical nature of this follicular attrition and re-activation by neighboring follicles produces a phenotype in which the mouse’s skin color at first uniformly oscillates between dark and light coloration, then begins to take on a remarkable striped appearance, with bands of pigmentation that originate from region under the forearms and travel across the body surface in all directions. These waves first appear at about three months after birth, and continue to arise and propagate throughout the life of the animal.

By tracking the movements of traveling waves in the Foxn1 mouse skin pattern, Kondo et al ascertained that their formation was fundamentally similar to that of waves generated by the BZ reaction. Although this finding gives no indication of the specific molecular mechanism at work in the Foxn1 phenotype, an understanding of the nature of its mathematical basis does provide clues for investigators in their work to identify the molecules responsible for normal and aberrant follicle development. And, as many other species demonstrate similar striping mechanisms, the current report may help to provide biologists with a mathematical model to explain this skin patterning phenomenon.